Transition to turbulence from spatially localised states

Previous Next

Transition to turbulence is usually considered as an undesirable event in both open flows (e.g. flow over an airplane wing) and closed flows (e.g. flows in pipelines) since turbulent flow is characterised by a significantly larger dissipation rate, i.e. transport loss, than laminar flow. As a result, more energy is required to move an object through turbulent fluid or transport fluid through the pipeline. Moreover, in all these processes, fluid interacts with some structure (a wing surface or a pipe) and sends its fluctuations to it. In some extreme cases, the intermittent nature of transition to turbulence and large difference between the amplitude of fluctuations in laminar and turbulent regions may damage the structure. It is then beneficial to keep the flow laminar as long as possible.

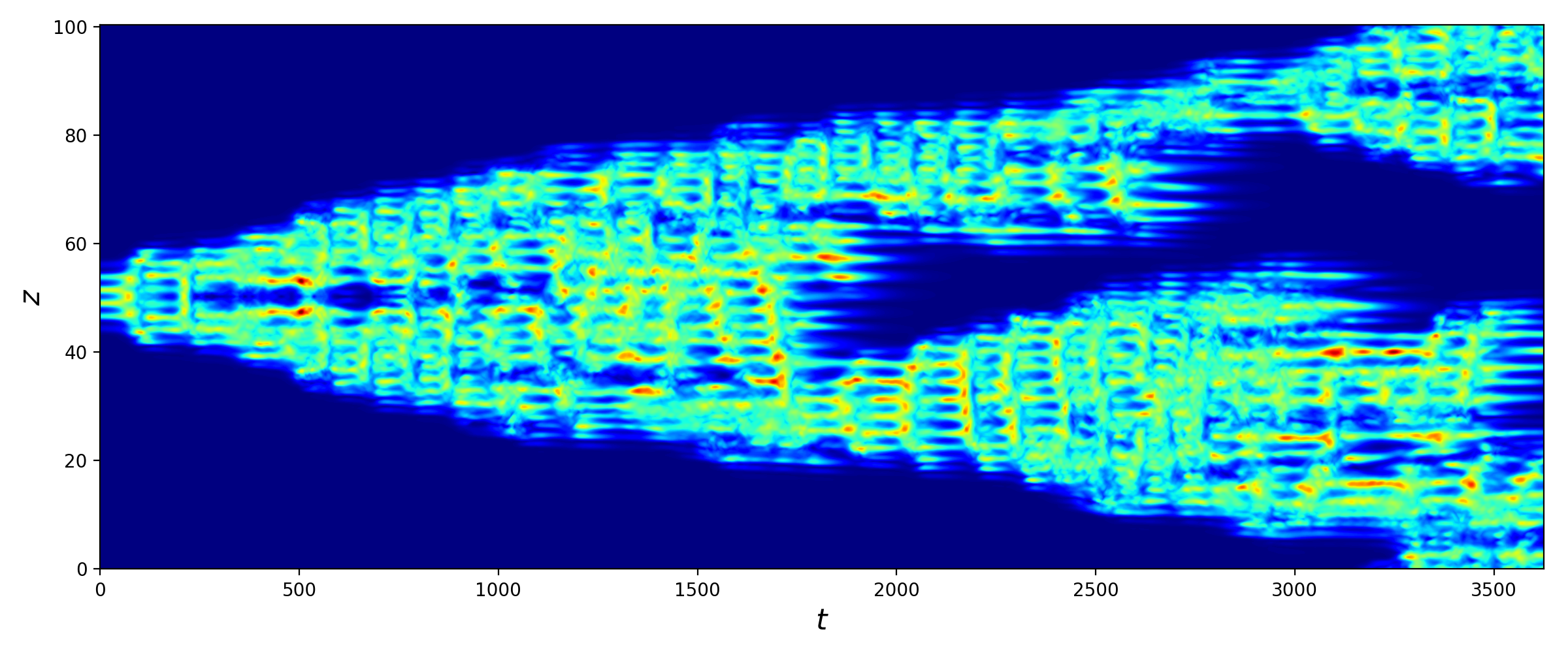
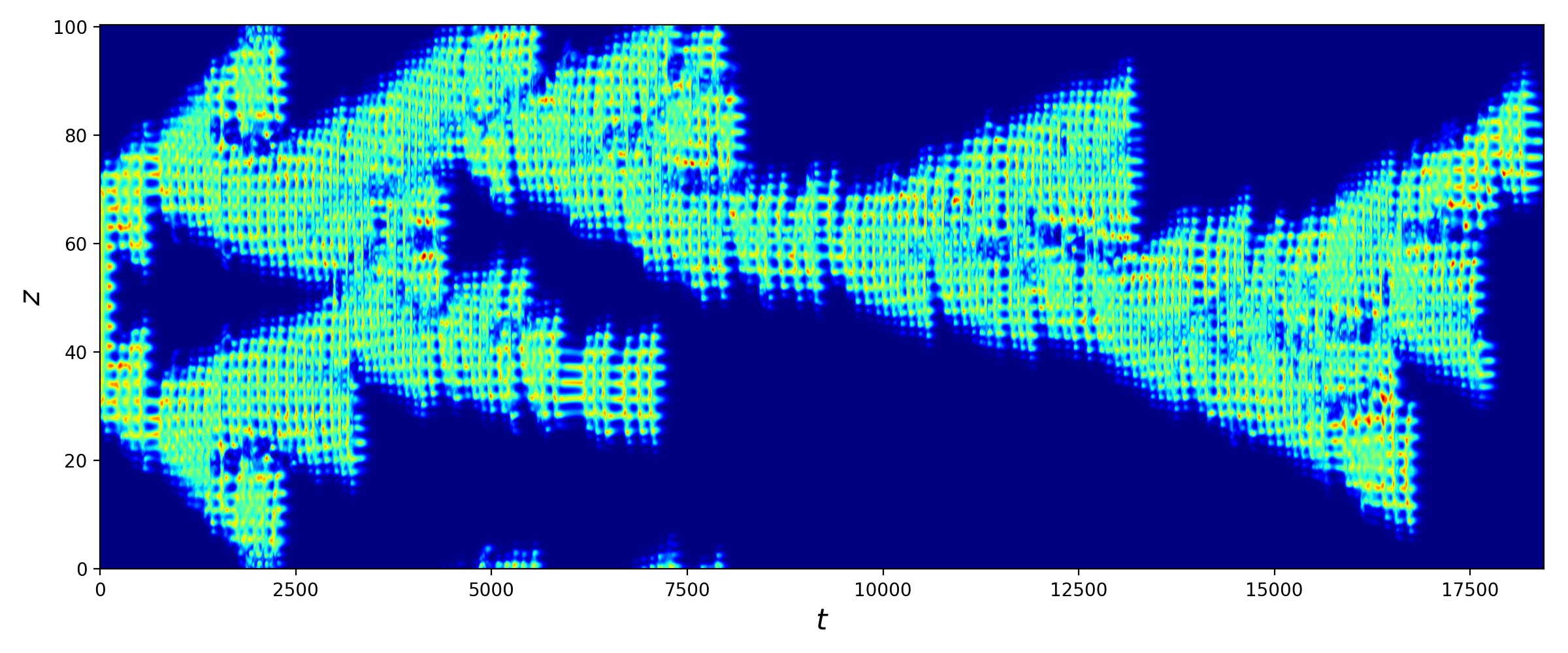
In our research, we investigate transition to turbulence in plane Couette flow -- a simple viscous flow between two parallel plates moving in mutually opposite directions with equal velocities. It has a linear laminar profile which is linearly stable for all Reynolds numbers, i.e., any infinitesimally small fluctuations around the laminar state will decay regardless the wall velocity. Consequently, one needs finite-amplitude perturbations to trigger turbulence. One of the options, considered in our research, is exact localised states which are made of streaks and rolls -- main ingredients of near-wall turbulent flows. We explore how these localised states, from the smallest (figure 1) to wide enough (figure 2) ones, transition to turbulence and how their transition can be suppressed.